いろいろ 1の平方根は 214250-1の平方根は
シェルスクリプト Mac ターミナルの基本的な使い方 操作方法 3
平方根 例題 平方根1 平方根2 循環小数1 循環小数2 平方根の大小1 平方根の大小2 平方根の積と商 ルートの変形1 ルートの変形2 有理化 ルートの乗法除法1 ルートの加法減法1 ルートの加法減法2 (変平方根のポイントは!・平方根とは「 2 乗の根っこ」のことで、プラスとマイナスの 2 個存在する!・ 0 の平方根は 0 のみ!・どんな数を 2 乗し
1の平方根は
1の平方根は-値を求める 64/169の平方根 Step 1 を に書き換えます。 正の実数と仮定して、累乗根の下から項を取り出します。 を に書き換えます。 正の実数と仮定して、累乗根の下から項を取り出しま平方の概算rootは四角のテーブルを使用できます。例えば、数値138は、144 = 12 ^ 2より小さいが、121 = 11 ^ 2より大きい。その結果、平方根は11と12の間になければなりません。平方根の場合

Linuxコマンド シェルで数値計算を実行 Linux入門 Webkaru
任意の正定値エルミート行列 P に対し、それ自身正定値エルミートとなる平方根は一意であり、これを主平方根 (unique square root, principal square root) と呼ぶが、しばしば記号 √ P や P 1/2 は平方根(へいほうこん)とは「2乗してaになる数」です。 aを2乗するとa 2 になります。 a 2 はaとaを2乗した数です。 よって、a 2 の平方根は「±a」です。 2乗と平方根は反対の関係だと覚えて平方根 求め方(ステップバイステップ): 平方根の計算の準備をするには、基本的な完全な平方根を覚えておく必要があります。 1、4、9、16、25、100のsqrtは、1、2、3、4、5、および10です
そもそも「平方根」という言葉自体どういう意味かわかりますか? 「平方」という言葉は「同じ数2つを掛け合わせること」という意味 で 「根」という言葉は「ある数を何乗かした 定義により √(1)=i です。1の平方根は2つありますが、その一方を√(1)とし、またiで表します。1の2つの平方根のうちどちらをiとするかは任意ですが、どちらを選んでも √( x=±1です。 (マイナスも忘れずに) √25ではなく5,と書くのと同じですよね。 √は可能な限り外します。
1の平方根はのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 | 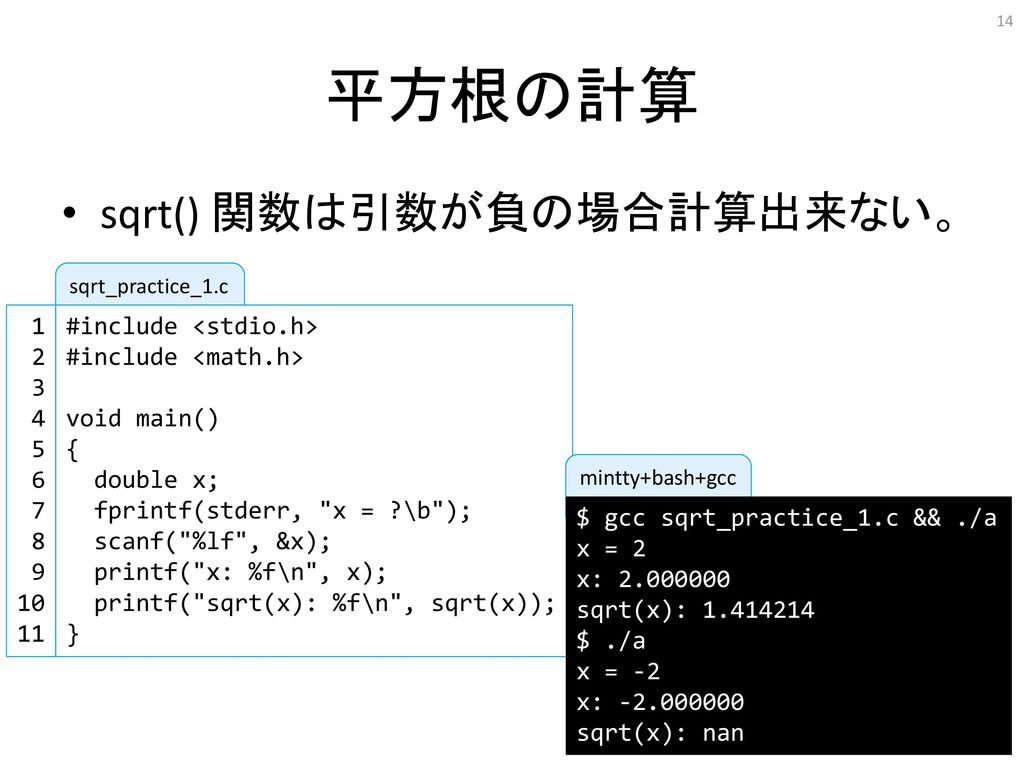 Cの平方根関数 |
Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 | Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 |  Cの平方根関数 | Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | 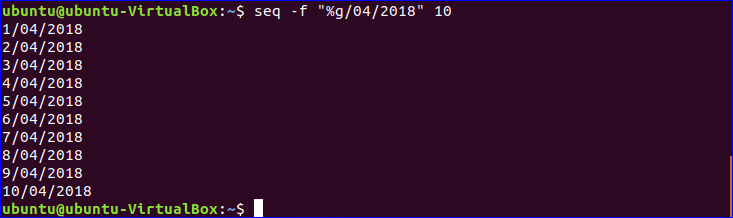 Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 | Cの平方根関数 | Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 | Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
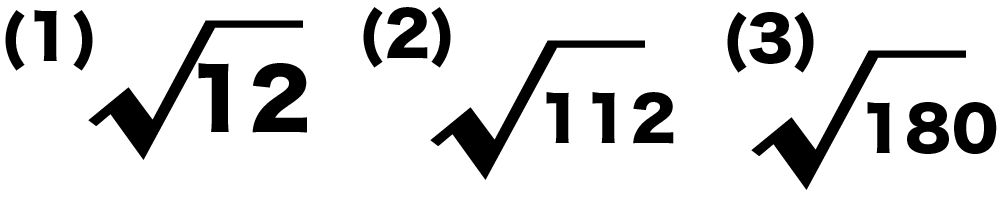 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 | 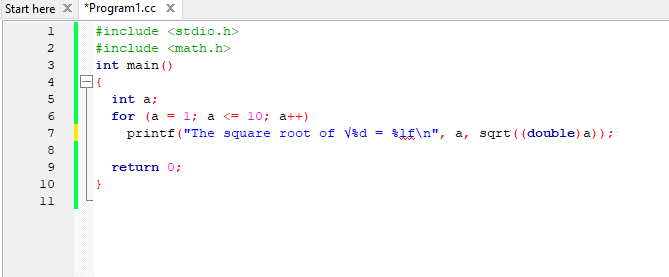 Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 | 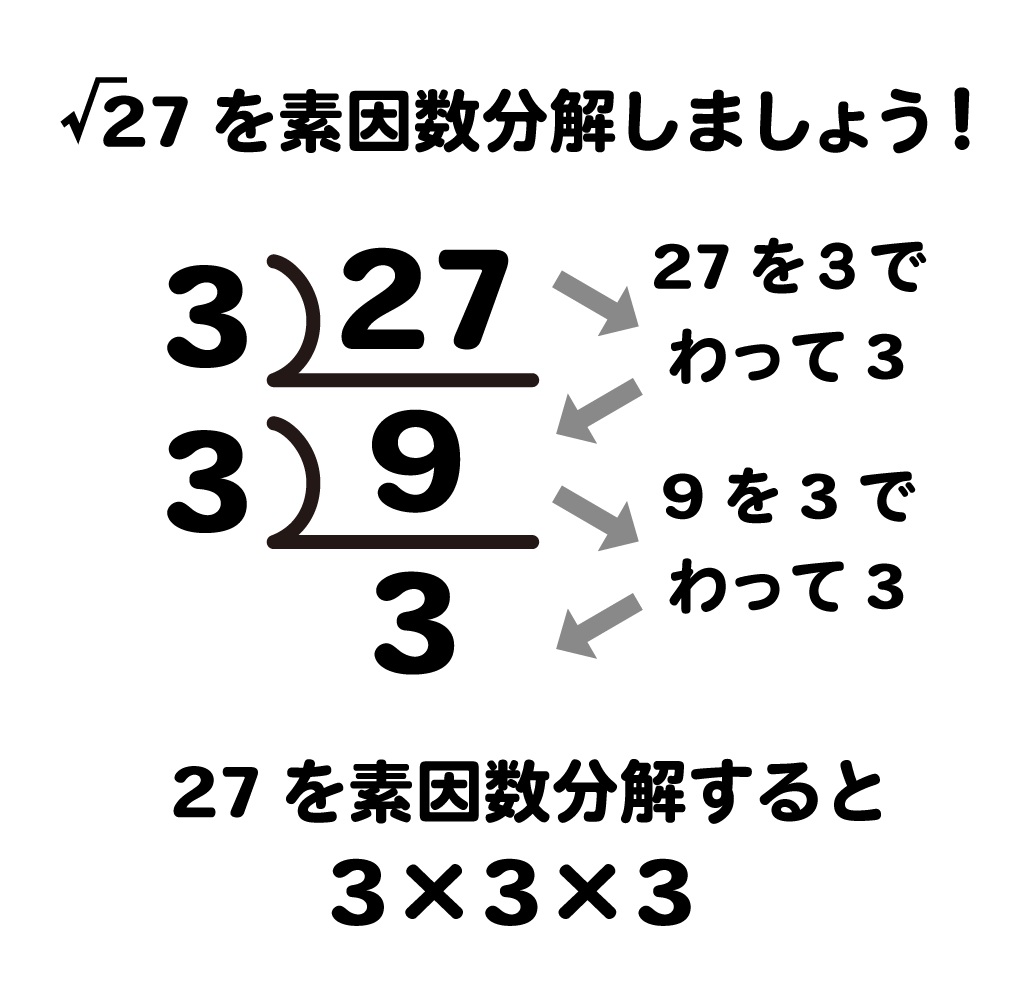 Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
Cの平方根関数 |  Cの平方根関数 |  Cの平方根関数 |
 Cの平方根関数 | Cの平方根関数 |  Cの平方根関数 |
「1の平方根は」の画像ギャラリー、詳細は各画像をクリックしてください。
 Cの平方根関数 |  Cの平方根関数 | 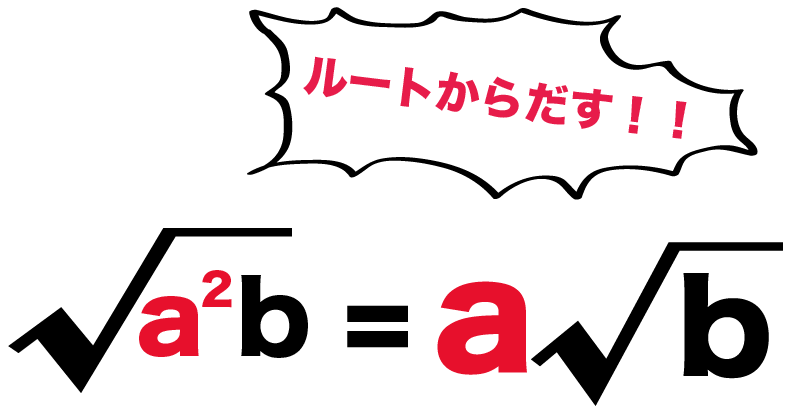 Cの平方根関数 |
Cの平方根関数 | Cの平方根関数 |
方法 関数を使って数値の平方根(ルート2)を計算するには、sqrt ()を使います。 まず、sqrt ()を呼び出します。 そして、sqrt ()の引数に数値を指定します。 #number=数値 result ここまでの結果をまとめると、 の平方根を とすれば、その の値は または となり、ここから の平方根は2つあり、その値は となることが判明しました! 実際に2乗してみても、 と
Incoming Term: 1の平方根は,
コメント
コメントを投稿